Materi Matematika SMP Kelas VII Bilangan Bulat

BILANGAN BULAT

1. Pengertian Bilangan Bulat 

Bilangan bulat adalah bilangan yang terdiri atas himpunan bilangan cacah dan bilangan bulat negatif.

·      Bilangan cacah yaitu 0, 1, 2, 3, 4, 5, 6, ...

·      Bilangan bulat negatif yaitu -1, -2, -3, -4. -5, -6, ...

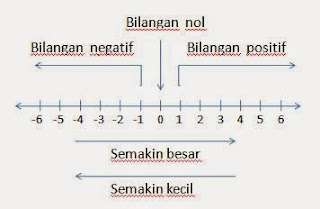
Jika digambarkan pada garis bilangan, letak bilangan bulat pada garis bilangan adalah sebagai  berikut:

Pada garis bilangan di atas, bilangan 1, 2, 3, 4, 5, 6, ... disebut bilangan bulat positif. Sedangkan bilangan -1, -2, -3, -4, -5, -6, ... disebut bilangan bulat negatif.

Bilangan bulat positif terletak di sebelah kanan nol, sedangkan bilangan bulat negatif terletak di sebelah kiri nol.

Jadi, kesimpulannya bilangan bulat adalah himpunan semua bilangan baik bilangan bulat negatif maupun bilangan bulat positif. Dan komponennya adalah ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... Semakin ke kiri semakin kecil dan sebaliknya semakin ke kanan semakin besar.

2. Operasi Hitung Pada Bilangan Bulat

Operasi pada bilangan bulat terdiri dari operasi:

1.Penjumlahan

Rumus penjumlahan pada bilangan bulat adalah :

(+a) + (+b)  = (+c)

(-a)  + (-b) = (-c)

(+a) + (-b)  = (+c) jika a>b

(+a) + (-b)  = (-c)  jika a<b

(-a)  + (+b) = (+c) jika a<b

(-a)  + (+b) = (-c)  jika a>b

2. Pengurangan

Rumus pengurangan pada bilangan bulat adalah :

(+a)  -  (+b)   = (+c)  jika a>b

(+a)  -  (+b)   = (-c)   jika a<b

(-a)   -  (-b)  = (+c)  jika a<b

(-a)   -  (-b)  = (-c)   jika a>b

(+a)  -  (-b)   = (+c)

(-a)   -  (+b)  = (-c)

3. Perkalian

Rumus perkalian pada bilangan bulat adalah:

(+a)  x (+b)    = (+c) 

(+a)  x (-b)    = (-c) 

(-a)   x (-b)   = (+c) 

(-a)   x (+b)   = (-c)

4. Pembagian

Rumus pembagian pada bilangan bulat adalah :

(+a)  : (+b)  = (+c)

(+a)  : (-b)  = (-c)

(-a)   : (+b) = (-c) 

(-a)   : (-b) = (+c) 

3.Menaksir Hasil Perkalian dan Pembagian Bilangan Bulat

Untuk menaksir hasil perkalian dan pembagian bilangan bulat ada dua cara, yaitu:

a. Untuk pembulatan ke angka puluhan terdekat.

o  Jika angka satuannya kurang dari 5, angka tersebut tidak dihitung atau dihilangkan.

o  Jika angka satuannya lebih dari atau sama dengan 5, angka tersebut dibulatkan ke atas menjadi puluhan.

b. Untuk pembulatan ke angka ratusan terdekat

o    Jika angka puluhannya kurang dari 5, angka puluhan dan satuan dihilangkan.

o  Jika angka puluhannya lebih dari atau sama dengan 5, angka puluhan tersebut dibulatkan ke atas menjadi ratusan.

Tetapi, aturan penaksiran bilangan bulat diatas juga berlaku untuk pembulatan ke angka ribuan terdekat, puluh ribuan terdekat, dan seterusnya.

4. Kelipatan dan Faktor

a. Kelipatan suatu bilangan

Kelipatan suatu bilangan dapat diartikan sebagai hasil kali bilangan tersebut dengan bilangan asli. Yang dimaksud bilangan asli adalah 1, 2, 3, 4, 5, ....

Lalu bagaimana menentukan kelipatan suatu bilangan?

Kita ambil contoh misanya bilangan 2 kelipatan dari berapa? Nah, bagaimana kita mencari? Kalikan bilangan 2 dengan angka 1, 2, 3, 4, 5 dan seterusnya secara berurutan.

1 x 2 = 2

2 x 2 = 4

3 x 2 = 6

4 x 2 = 8

5 x 2 = 10

6 x 2 = 12

Karna angka yang bercetak tebal itu adalah hasil perkaliannya,maka itulah kelipatanya.  Jadi, bilangan kelipatan 2 adalah 2,4,6,8,10,12, dan seterusnya.

Kita bisa lebih mudah menentukan kelipatan bilangan bulat dengan melihat bahkan menghapal perkalian berikut:

b. Faktor suatu bilangan

Faktor suatu bilangan adalah suatu bilangan yang membagi bilangan lain menghasilkan bilangan asli.

Lalu,  bagaimana mencari faktor suatu bilangan ?

Kita ambil contoh misalnya angka 5. Kita bagi bilangan 5 dengan bilangan asli dengan berurutan.

5 : 1 = 5

5 : 2 = 2,5 (bukan faktor bilangan) 

5 : 3 = 1,6 (bukan faktor bilangan) 

5 : 4 = 1,25 (bukan faktor bilangan) 

5 : 5 = 1

Kenapa bila hasil desimal bukan faktor bilangan?  Karena faktor harus mendapatkan bilangan asli. Jadi, Faktor adalah 1 dan 5.

5.Perpangkatan Bilangan Bulat

Di dalam perpangkatan bilangan bulat ada berbagai macam sistem operasinya misalnya perkalian pangkat, pembagian pangkat, pangkat nol, pangkat negatif,dan sebagainya. Berikut rumus lengkapnya:

6.Operasi hitung pada bilangan bulat

Dalam menyelesaikan sistem operasi campuran terdapat aturan-aturan yang dilakukan dalam pengerjaan soal yaitu : 

·      Penjumlahan dan pengurangan setingkat. Maka kerjakan berurutan dari kiri

·      Perkalian dan pembagian setingkat. Maka dikerjakan berurutan dari kiri

·      Derajat perkalian dan pembagian lebih tinggi daripada penjumlahan dan pengurangan maka perkalian dan pembagian dikerjakan lebih dulu.

·      Operasi hitung yang terdapat dalam tanda kurung dikerjakan lebih dahulu.